https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
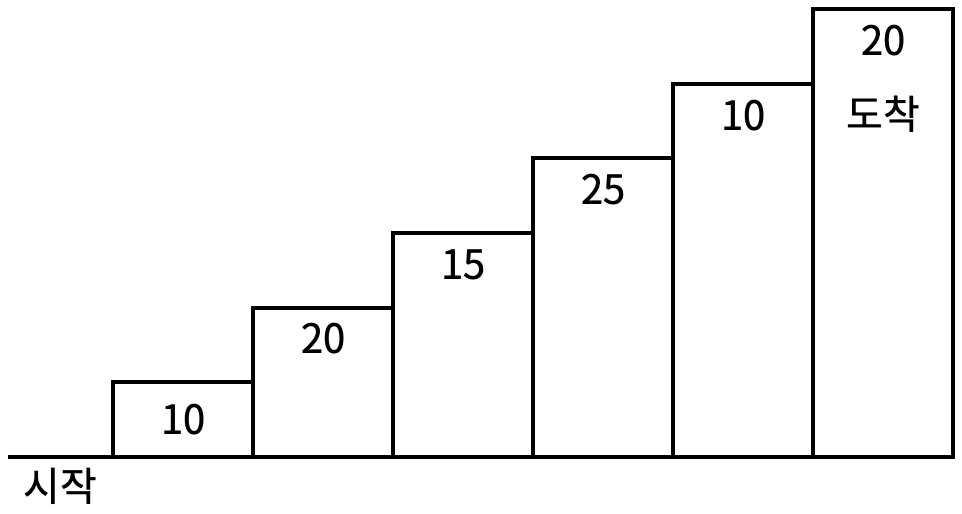
<그림 1>
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
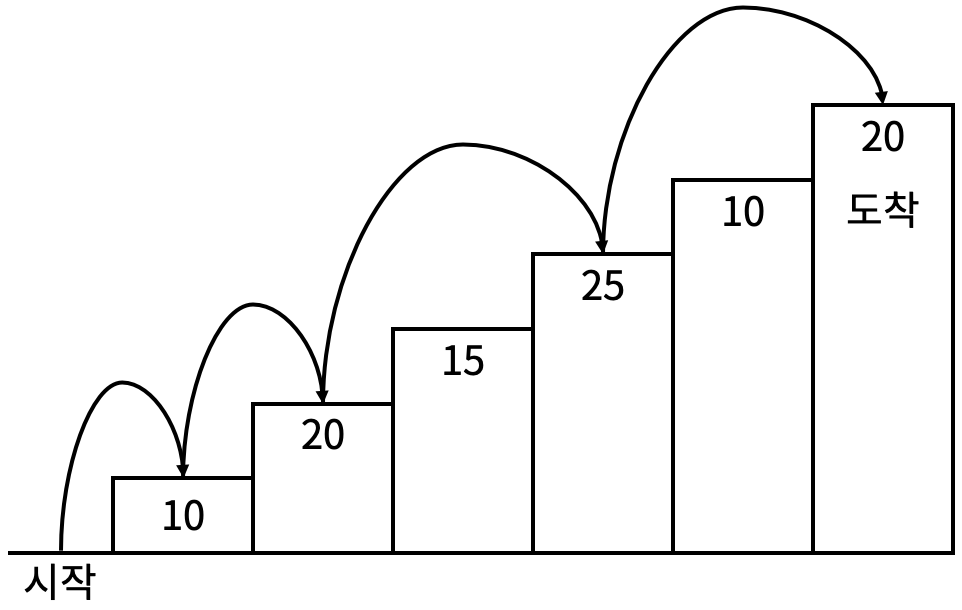
<그림 2>
계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
해결코드
n = int(input()) #6
num = [0 for i in range(301)]
li = [0 for i in range(301)]
for i in range(n):
num[i] = int(input())
li[0] = num[0] #10
li[1] = num[0] + num[1] #30
li[2] = max(num[1] + num[2], num[0] + num[2]) #45
for i in range(3, n):
li[i] = max(li[i - 3] + num[i - 1] + num[i], #10+15+25
li[i - 2] + num[i])
print(li[n - 1])문제풀이
이 문제 역시 dp를 이용하여 풀어야 한다.
생각해야 될 게 연속으로 세 개의 계단을 밟을 수는 없다.
두 개의 계단을 연속으로 밟았으면 다음은 바로다음 계단을 밟을 수 없고 두개위의 계단을 밟아야한다.
그리고 마지막 계단을 무조건 밟아야 한다고 했으니
마지막 계단 이전 계단의 경우의 수가 두 가지 나온다.
1. 마지막 계단 바로 전 계단을 밟는 것 ex) 10/10/10/10/10/10
2. 마지막 계단 두 칸 밑의 계단을 밟는 것 ex) 10/10/10/10/10/10
1번의 경우 마지막 계단과 바로 전 계단을 밟았으므로(2개 연속으로 밟은것) 전전계단은 전계단
두칸 밑의 계단이어야 한다. ex) 10/10/10/10/10/10
2번의 경우 전전계단은 상관 안해도 된다. ex) 10/10/10/10/10/10 ex) 10/10/10/10/10/10
코드를 살펴보자
일단 n에 숫자 개수를 받아준다.
계단의 개수가 300개 이하라고 했으므로 시간을 줄이기 위해
그냥 300개의 모든계단 리스트를 만들어서 0으로 초기화한다.(num 리스트)
li라는 리스트는 계단에 적혀있는 숫자의 합을 저장한다. 똑같이 300개의 리스트를 0으로 초기화
그리고 for문을 돌려 num[0]부터 num[n]까지 차근차근 계단에 적힌 수를 받아주도록 한다.
li에는 num값 합의 최대값을 저장한다고 했다.
예를 들어 li[0]은 num[0]이랑 같다.(첫번째 계단을 밟는 경우는 한 가지 밖에 없다)
li[1]은 num[0]이랑 num[1]의 합을 넣어준다.
(두 번째 계단을 밟는 경우중 최대 값은 첫 번째 계단을 밟지 않고 두 번쨰 계단을 밟거나
첫 번째 계단도 밟고 두 번째 계단도 밟는 경우인데 첫 번째 계단 값이 음수가 아닌 이상
둘 다 밟는게 최대값일 수밖에 없다)
li[2]는 세번째 계단을 밟게될 때 최대값을 넣어준다.
두 가지의 경우가 있는데 두 번째 계단을 밟고 세 번째 계단을 밟는 경우와
첫 번째 계단을 밟고 세 번째 계단을 밟는 경우가 있는데
이 두 경우 중 더 큰 값을 li[2]에 넣으면 된다.
*참고로 li[n]일때 n번째 계단은 무조건 밟아야 한다.(마지막 계단)
이렇게 해서 기본 값은 모두 세팅이 되었고
이제 for문을 돌리는데 li[2]까지 완성이 되었으니 li[3]부터 li[n]까지 for문을 돌려야한다.
앞에서 말헀듯이 무조건 마지막 계단을 밟게 되니
마지막 계단 전계단에 대해 경우를 생각하면
1. 마지막 계단 바로 전 계단을 밟는 것 ex) 10/10/10/10/10/10
2. 마지막 계단 두 칸 밑의 계단을 밟는 것 ex) 10/10/10/10/10/10
1번의 경우 li[i-3] + num[i-1] + num[i]
--> 마지막 계단(num[i])+마지막계단 전계단(num[i-1]) + 전계단 두칸밑 계단까지의 합(li[i-3])
2번의 경우 li[i-2] + num[i]
--> 마지막 계단(num[i]) + 마지막계단 두칸밑계단까지의 합(li[i-2])
이 두가지 경우 중 큰 값을 li[i]에 넣으면 되는 원리이다.
결과 값은 li[n-1]을 출력하는데 이유는 li가 li[0]부터 시작하기 때문이다 ^^
'Algorithm' 카테고리의 다른 글
| [알고리즘] 백준 9375 패션왕 신해빈 (파이썬 풀이) (0) | 2022.02.07 |
|---|---|
| [알고리즘] 백준 11047 동전 0 (파이썬 풀이) (0) | 2022.02.06 |
| [알고리즘 ] 백준 1463 (파이썬 풀이) (0) | 2022.02.04 |
| [알고리즘] 백준 9095 (파이썬 풀이) (0) | 2022.02.03 |
| [알고리즘] 백준 11723 (파이썬 풀이) (0) | 2022.02.02 |
댓글